Emissions de gaz à effet de serre, économie, intensité énergétique, population… Il y aurait un lien entre ces diverses grandeurs, que chacun – physiciens, économistes ou politiques, ingénieurs, démographes – aime à utiliser dans son coin ? Une équation, géniale parce que si simple (et, comme on va le voir, si terrible !), et que la rumeur attribue à un professeur japonais dénommé Kaya (ce qui est sûr, c’est que le Professeur Kaya en question est un chercheur connu pour les questions de politique énergétique), permet de relier entre elles ces notions, même si pour la majorité de mes concitoyens « on ne voit pas le rapport avec la choucroute ».
Cette équation part du principe, très simple – et dont des générations de collégiens se souviennent sûrement ! – que l’on peut toujours multiplier ou diviser par un même nombre chaque coté d’une égalité.
Notre égalité de départ est on ne peut plus évidente. Appelons CO2 les émissions mondiales de gaz carbonique, le principal gaz à effet de serre d’origine humaine, et nous pouvons écrire qu’elles sont égales à elles-mêmes, ce sur quoi on devrait être d’accord :
CO2= CO2
Jusque là, tout le monde devrait suivre ! Appelons maintenant TEP la quantité d’énergie consommée dans le monde (par référence à l’unité « tep », ou « tonne équivalent pétrole », généralement utilisée quand on parle d’énergie). Tout le monde sait que, quand nous avons une égalité, il est possible de multiplier et diviser un des côtés par n’importe quoi de non nul. TEP étant non nul, nous pouvons, de l’un des côtés, à la fois multiplier et diviser CO2 par TEP, ce qui donne :
CO2= \frac{CO2} {TEP}\times{TEP}
Quel intérêt ? C’est que nous venons juste d’écrire que :
\text{\scriptsize{Emissions de GES }}=\text{ \scriptsize{Contenu en GES de l'energie} }\times \text{\scriptsize{Quantite d'energie consommee}}
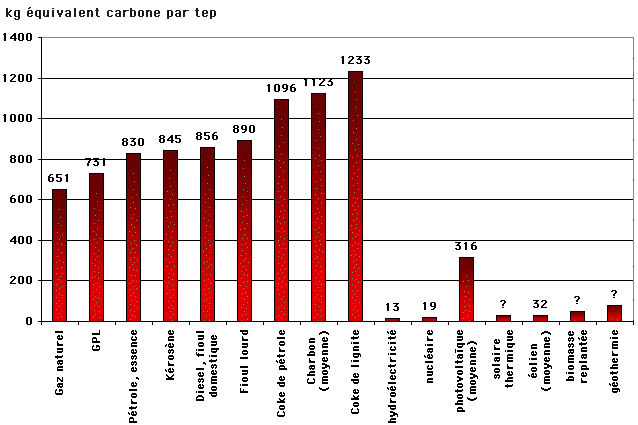
« Contenu en gaz à effet de serre » (en fait essentiellement « contenu en gaz carbonique ») par tonne équivalent pétrole d’énergie finale pour diverses énergies.
L’électricité est convertie sur l’équivalence énergie finale (1 TEP = 11,6 MWh).
Les points d’interrogation signifient que j’ai une vague idée de l’ordre de grandeur, mais que les chiffres précis varient d’une analyse à l’autre.
Ce premier graphique permet déjà de voir que, pour une consommation énergétique donnée, les émissions de CO2 dépendront beaucoup de la répartition des diverses sources que nous décidons d’avoir (ou pouvons avoir….). Pour information, l’essentiel de l’énergie que nous consommons actuellement dans le monde émet du CO2 (graphique ci-dessous), et la seule manière de faire baisser le « contenu en gaz carbonique de l’énergie » est de faire croître la part des énergies « sans carbone » (renouvelables et nucléaire) dans le mix.
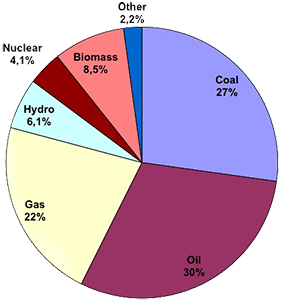
Part de chaque source d’énergie dans l’approvisionnement énergétique « primaire » de la planète en 2012.
L’énergie « primaire » est celle qui est à notre disposition dans le monde qui nous entoure (pétrole brut, charbon brut, gaz brut, bois et végétaux, noyaux d’uranium, chutes d’eau, rayons du soleil, chaleur des entrailles de la terre, etc).
L’énergie que nous utilisons au quotidien n’est pas de l’énergie primaire, mais « finale » : carburants raffinés, gaz purifié, électricité (qui n’est pas une énergie primaire, et qui est aussi « propre » que l’énergie primaire avec laquelle elle est fabriquée), etc. L’hydrogène, si nous l’utilisons un jour, est aussi une énergie finale, et donc aussi « propre » que l’énergie primaire utilisée pour la fabriquer.
Les énergies « sans carbone » représentent environ 20% du total : bois, hydro, nucléaire, autres.
Source : BP Statistical Review, 2013
Nous pouvons alors répéter l’exercice consistant à multiplier et diviser par le même nombre. Multiplions et divisons le côté droit par PIB, c’est à dire le produit intérieur brut, autrement dit l’unité qui mesure l’activité économique.
CO2= \frac{CO2} {TEP}\times\frac{TEP} {PIB}\times{PIB}
Nous avons maintenant écrit :
\text{\scriptsize{Emissions de GES }}=\text{\scriptsize{Contenu en GES de l'energie} }\times\text{\scriptsize{Intensite energetique de l'economie}}\times\text{\scriptsize{PIB}}
En effet, la division de l’énergie par le PIB (TEP/PIB) porte le nom de « intensité énergétique de l’économie » : c’est la quantité d’énergie qu’il faut utiliser pour produire un dollar (ou un euro) de biens ou services. L’intensité énergétique de l’économie est sur une pente descendante depuis le début de l’ère industrielle, en première approximation, parce que l’efficacité de l’économie n’a cessé de croître.
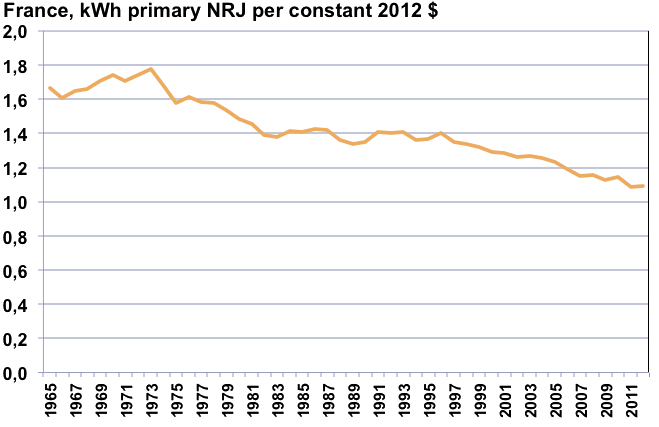
Quantité d’énergie consommée par dollar constant de PIB en France depuis 1965.
Ce que dit cette courbe est que pour produire un euro de PIB en France en 2000 il faut utiliser environ 35% d’énergie en moins qu’en 1970.
Calcul de l’auteur sur sources BP Statistical Review, 2013, et World Bank, 2013
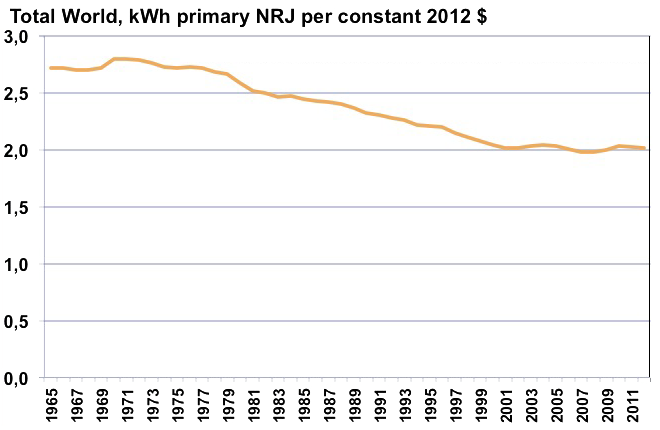
Quantité d’énergie consommée par dollar constant de PIB dans le monde depuis 1965.
Ce que dit cette courbe est que pour produire un dollar de PIB en 2012 dans le monde il faut utiliser environ 25% d’énergie en moins qu’en 1970.
Notez que l’efficacité énergétique ne s’améliore pas entre 2000 et 2012.
Calcul de l’auteur sur sources BP Statistical Review, 2013, et World Bank, 2013
Bien que cette donnée baisse, il est facile de voir dès à présent que de se focaliser sur cette seule partie de « l’équation » est oublier le reste, et notamment évacuer dès à présent le débat suivant : est-on sûr que si l’intensité énergétique du PIB diminue ce n’est pas essentiellement… parce que PIB augmente plus vite que la consommation d’énergie ? (et en fait c’est bien ce qui se passe).
Enfin il nous reste à inclure la démographie pour que la discussion puisse devenir intéressante. Appelons POP la population, et multiplions et divisons la partie droite de l’égalité par ce terme, ce qui donne :
CO2= \frac{CO2} {TEP}\times \frac{TEP} {PIB}\times \frac{PIB} {POP} \times{POP}
Traduit en Français, nous avons maintenant écrit :
\text{\scriptsize{Emissions de GES }}=\text{\scriptsize{Contenu en GES de l'energie} }\times \text{\scriptsize{Intensite energetique de l'economie}}\times \text{\scriptsize{Production par personne}}\times \text{\scriptsize{Population}}
Le terme PIB/POP est en effet d’usage très courant, et s’appelle indistinctement « production par personne », ou encore … « richesse » (bien que le PIB ne mesure en rien la richesse mais juste la rémunération annuelle de l’humanité). Et voilà comment il est possible d’exprimer les émissions de CO2 (mais le raisonnement général pourrait s’appliquer à l’ensemble des gaz à effet de serre) en fonction de paramètres qui vont permettre de savoir si la dématérialisation est à portée de la main. Maintenant, la discussion intéressante commence !
Que faire de tout cela ?
Bon, voici une belle équation. Et après ? Après nous voyons déjà que toute discussion portant sur un seul des facteurs de droite n’est pas suffisante pour parvenir à une conclusion sur les émissions (à gauche). Ainsi, quand Bush a annoncé, en 2003 (ou peu avant), qu’il allait diminuer l’intensité énergétique de l’économie américaine de 18% en 10 ans, il est facile de voir que cela ne porte que sur l’un des termes de cette égalité (TEP/PIB). Et le reste ? Si la production économique par personne (PIB/POP) augmente de 25% dans le même temps (ce qui représente une croissance de 2,5% par an, soit un objectif conservateur pour n’importe quel gouvernement), avec une population (POP) qui augmente de quelques % dans le même temps (simple prolongation des tendances aux USA), et un contenu en carbone qui reste constant (assertion raisonnable compte tenu des tendances actuelles aux USA, particulièrement dans le secteur de l’électricité), le résultat sera une hausse des émissions de CO2, pas une diminution !
Revenons à nos moutons :
Il est établi que pour cesser d’enrichir l’atmosphère en gaz carbonique il faut diviser les émissions mondiales de 2010 par 3 au moins.
Si nous voulons éviter des conséquences potentiellement très désagréables, il faut y arriver à l’horizon de quelques décennies, disons d’ici 2050. Mais la très mauvaise nouvelle est que cela arrivera même si nous ne le voulons pas, car la terre est finie.
En effet, les émissions de CO2 proviennent des hydrocarbures que nous consommons et des forêts que nous défrichons, et tout cela est en quantités données une fois pour toutes : le stock d’hydrocarbures est donné une fois pour toutes, et la surface maximale de forêts également. De ce seul fait, les mathématiques nous enseignent que les émissions vont passer par un maximum et inexorablement décroître avec le temps ensuite (en tendance lourde, évidemment). En langage mathématique, on dit que les émissions de CO2 n’ont pas d’autre choix que de tendre vers zéro à l’infini, et cela signifie en particulier qu’il viendra un jour où ces émissions seront devenues « pour toujours » inférieures au tiers des émissions actuelles, et même « un jour » inférieures « pour toujours » au quart des émissions actuelles, etc.
Bref, dans notre équation ci-dessus nous devons donc viser une division de la partie gauche de l’égalité par 3, et même si nous ne la visons pas nous l’aurons un jour. Comme le grand mérite d’une égalité est que les deux termes doivent être égaux (si si !), cela signifie que l’ensemble des termes de droite doit aussi être divisé par 3 – ou le sera « un jour » même si cela ne nous plait pas.
Qu’allons nous donc diviser par 3 ou par autre chose ?
- Peut-on diviser la population mondiale par 3 ?
Le décider de manière planifiée et rapide (40 ans c’est court) portant le nom désagréable de massacre ou de génocide, il est peu probable que cela constitue une option considérée de manière sérieuse. Et compter sur une épidémie (qui devrait aussi diviser par 3 la population des pays riches, gros émetteurs) pour faire le travail à notre place peut difficilement être souhaité !En fait, si nous allons demander leur avis aux démographes, ces derniers disent volontiers que la population s’achemine plutôt vers une multiplication par 1,3 d’ici 40 ans. Cette prolongation est bien sûr valide si aucune régulation n’intervient : aucun scénario démographique ne fait autre chose que de l’ajustement de taux de mortalité et de fécondité, et ces taux ne sont jamais « programmés » pour refléter une évolution brutale que nous ne pouvons pourtant pas exclure (chute d’un météorite, guerre nucléaire et retour à la barbarie, épidémie massive, et toute savante combinaison de petits malheurs, y compris les conséquences alimentaires, sanitaires ou politiques du changement climatique).
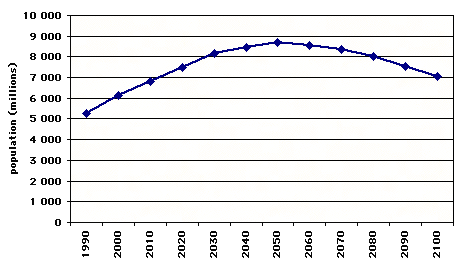
Evolution de la population mondiale dans les scénarios d’émission de gaz à effet de serre de la famille A1.
Source : GIEC
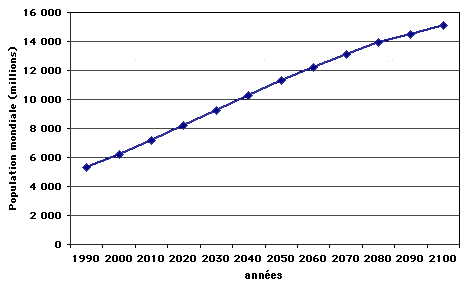
Evolution de la population mondiale dans les scénarios d’émission de gaz à effet de serre de la famille A2.
Source : GIEC
Ces deux scénarios considèrent que la population mondiale atteindra 9 milliards de personnes, à quelque chose près, en 2050. Ces scénarios sont bien sûr discutables, mais ils représentent la vision « conventionnelle » dont il est intéressant de voir si elle est un tant soit peu compatible avec notre problème !
Puisque la population est tendanciellement multipliée par 1,3 alors que les émissions doivent être divisées par 3, cela signifie que l’ensemble des autres facteurs doit être divisé par 4 (les mathématiques, c’est bête comme chou).
- Peut-on alors diviser la production par habitant (PIB/POP) par 4 ?
Cela supposerait un choix délibéré de récession, évolution qui comporte certes quelques avocats (les partisans de la « décroissance » par exemple), mais on ne peut pas dire que cela corresponde à la « vision conventionnelle » de l’avenir de l’immense majorité de mes concitoyens (ce qui ne veut pas dire que la récession soit peu probable ! Cela signifie juste que la mise au régime « à froid » par les élus pour se prémunir contre un danger futur n’est pas l’attitude la plus courante). Par exemple, les propos électoraux – approuvés par la masse – de n’importe quel ministre ou président de la république sont en général très favorables à la hausse du pouvoir d’achat, or le pouvoir d’achat, à quelques bricoles près, c’est très exactement le PIB par personne.Dit autrement, nous souhaitons tous les jours que « la croissance » perdure, chez les riches comme chez les pauvres.
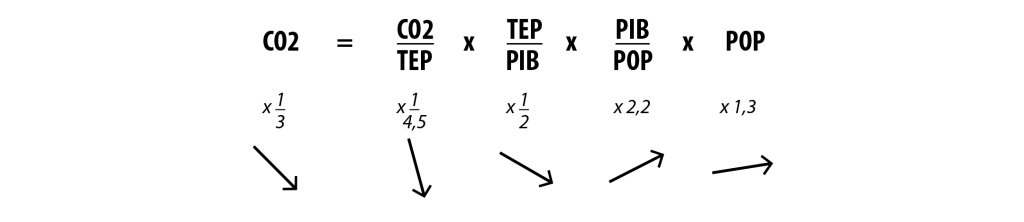
Une augmentation de 2% par an du PIB par habitant, ce que tout élu tente d’obtenir lorsqu’il est en fonctions, multiplie cette valeur par 2,2 en 40 ans, ce qui signifie que le reste des autres facteurs de la partie droite de notre équation doit alors être divisé par 9 : à gauche, on divise par 3 ; à droite on multiplie par 3 le PIB mondial (cette multiplication par 3 se décomposant en x 1,33 pour la population et x 2,2 pour le PIB par personne).Rappelons, avant de passer à la suite, que l’augmentation du PIB désigne uniquement la croissance de la production de produits ou services faits de la main de l’homme, mais compte pour zéro la disparition concomitante et irréversible des ressources non renouvelables – minerais, énergies fossiles… – qui ont été nécessaires pour leur mise à disposition. La prise en compte de ce deuxième facteur à un niveau pas plus idiot qu’un autre pourrait nous amener à considérer que nous sommes déjà en décroissance…
En « vision conventionnelle de l’avenir », nous voici donc avec une division par 9 – disons 10 pour nous simplifier la vie – à réaliser sur le produit :
\text{\scriptsize{Contenu en GES de l'energie} }\times \text{\scriptsize{Intensite energetique de l'economie}}
- L’intensité énergétique peut-elle être divisée par 10 en 40 ans ? Elle a baissé de 30% en 35 ans dans le monde (graphiques sur l’intensité énergétique de l’économie ci-dessus) ; la prolongation d’un taux de diminution identique amène à une réduction de 35% en 40 ans, mais c’est une hypothèse qui a des côtés optimistes, parce que ce sont les premiers efforts qui sont les plus faciles à faire. Passons, et supposons que nous puissions gagner un facteur 2 d’ici 2050. L’intensité énergétique étant alors de 50% de ce qu’elle est aujourd’hui, c’est donc un facteur 4 à 5 par lequel il faut diviser le contenu en GES de l’énergie (GES/TEP).
- Dit autrement, il faut donc diviser le « contenu en gaz carbonique de l’énergie » par un facteur 4 au moins, alors que ce « contenu en gaz carbonique de l’énergie » a juste diminué de 10% sur les 40 dernières années…
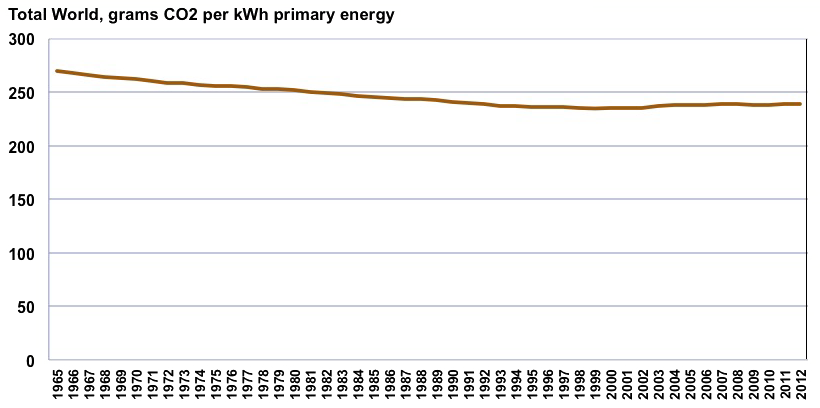
Grammes de CO2 émis par kWh d’énergie primaire consommée dans le monde depuis 1965.
On note que depuis 2000 cet indicateur s’est légèrement dégradé à cause de la croissance rapide du charbon en Chine. Et il faudrait que cette « intensité en carbone de l’énergie » perde 80% en 40 ans !
Calcul de l’auteur sur sources BP Statistical Review, 2013, et World Bank, 2013
- Au surplus il faut parvenir à cette « décarbonisation de l’énergie » en multipliant l’approvisionnement par 1,5 (car le produit des trois termes
\text{\scriptsize{Intensite energetique de l'economie}}\times \text{\scriptsize{Production par personne}}\times \text{\scriptsize{Population}}
n’est rien d’autre que la consommation d’énergie). Comme aujourd’hui les énergies « sans carbone » font environ 18% du total mondial (en équivalent primaire), cela signifie que dans le même temps :
– l’approvisionnement en provenance des fossiles doit baisser de 2,7% par an entre 2010 et 2050 (ce qui ne nécessite qu’une chose : une hausse du prix réel de l’énergie fossile)
– l’approvisionnement en provenance des renouvelables et du nucléaire doit augmenter de 5% par an, pour être multiplié par 7 en 40 ans.
Une représentation graphique de la chose est proposée ci-dessous.
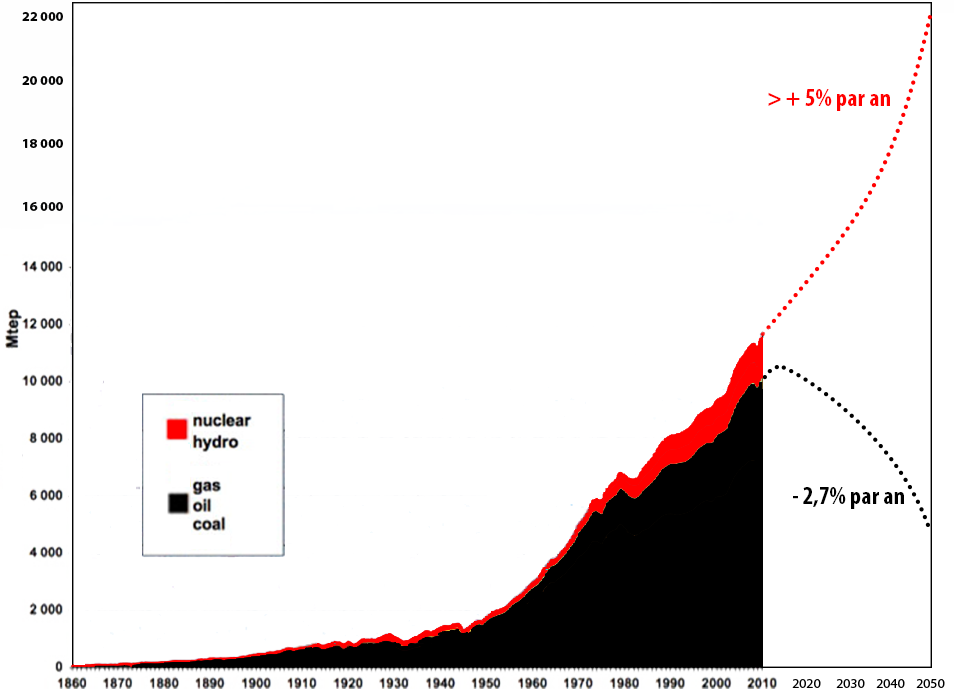
Représentation graphique approximative de l’approvisionnement énergétique mondial – en millions de tonnes équivalent pétrole – pour poursuivre la croissance économique avec en 2050 des émissions divisées par trois par rapport à 2010.
NB : le bois n’est pas représenté sur ce graphique (mais est pris en compte dans le calcul du taux de croissance des renouvelables), et les renouvelables hors bois sont limitées à l’hydroélectricité (ce qui en 2010 est une assez bonne approximation).
Question : peut-on multiplier la contribution du nucléaire et des renouvelables par 7 en 40 ans ? (évidemment si on se passe du nucléaire cela change un poil la contribution des renouvelables, on y vient plus bas). Commençons par les renouvelables, qui en 2010 fournissent à l’humanité un gros 15% de sa consommation d’énergie (électricité en équivalence primaire), soit 2,1 milliard de tonnes équivalent pétrole.
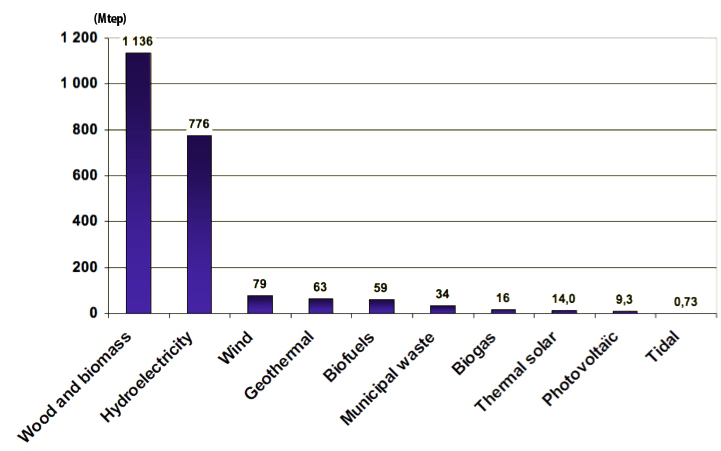
Contributions estimées des énergies renouvelables au bilan énergétique mondial en 2010, en millions de tonnes équivalent pétrole.
(1 tonne équivalent pétrole = 11600 kWh ; l’électricité est convertie sur l’équivalence énergie finale).
Hors bois, la consommation d’énergie de l’humanité est de 12,4 milliards de tonnes équivalent pétrole (soit 12 400 millions, si je sais encore compter), ce qui permet de constater que le bois fait à peu près 10% du total mondial, l’hydroélectricité un gros 5%, et ensuite tout le reste est marginal.
Sources : diverses
Pouvons-nous multiplier cet ensemble par 7 ? Pour se faire une idée, continuons donc notre petit jeu idiot des règles de trois, en regardant source par source :
- Une énergie du bois multipliée par 7 doit alors fournir 8 milliards de tonnes équivalent pétrole par an, sans engendrer de déforestation. Il se trouve que, dès à présent, avec « juste » 10% de l’énergie mondiale qui en vient, l’utilisation du bois est déjà une source de déforestation significative (10% à 20% du bois consommé dans le monde provient déjà de la déforestation).
Sachant qu’un hectare de forêt fournit environ 3 tonnes équivalent pétrole par an en mode « renouvelable » (mode « renouvelable » signifie que ce qui est coupé est uniquement ce qui a poussé dans l’année) en moyenne mondiale, avoir 8 milliards de tonnes équivalent pétrole de bois (ou de biomasse) signifie qu’il faut avoir 33 millions de km² de forêts dédiées à la production de bois-énergie, soit 20% des terres émergées, ou… à peu près l’équivalent des forêts actuelles. Si nous utilisons des cultures plus « rentables » que le bois, on peut monter à 5 à 6 tonnes équivalent pétrole par hectare et par an en production nette, mais cela représente toujours 50% des surfaces couvertes de forêts ou des terres agricoles.
Pas si facile… et si nous voulons utiliser le désert pour y faire pousser des algues, il faut faire des calculs qui tiennent la route pour avoir une idée de ce que cela représente, sans compter que nous aurons un débat sur le taux de croissance annuel moyen à soutenir sur une longue période, et qui se présente comme pour l’éolien, discuté plus bas.
- Dans le même temps il faudrait multiplier l’hydroélectricité par 7, ce qui signifie multiplier par 7 les turbinages au fil de l’eau et les lacs de barrage. Dans un certain nombre de zones géographiques c’est peut-être envisageable, au prix de nuisances environnementales non négligeables (le barrage des Trois Gorges, parfaitement renouvelable, a néanmoins demandé le déplacement de 1 million de personnes), mais sûrement pas en Europe, où l’essentiel de ce qui est équipable est équipé.
- Si nous passons ensuite aux autres sources (biogaz, biocarburants, éolien, photovoltaïque, etc), même multipliées par 7 elles restent parfaitement marginales, et c’est par bien plus de 7 qu’il faudrait les multiplier dans les 40 ans qui viennent pour combler la différence. Incidemment nous pouvons constater que pour les énergies renouvelables, il y a une loi qui fonctionne assez bien : leur importance dans l’approvisionnement énergétique mondial est inversement proportionnelle à leur place dans les médias !
- Admettons que nous voulions tout arranger avec juste de l’éolien, énergie très en vogue chez les partisans des renouvelables, du moins en Europe. Si nous voulons arriver à 22 milliards de tonnes équivalent pétrole en 2050 en divisant le CO2 par trois et en utilisant juste l’éolien dans la croissance des renouvelables, il nous faut augmenter cette source d’environ 14% par an sur 40 ans, pour parvenir à une multiplication par… 160 en 2050, ou encore 12,7 milliards de tonnes équivalent pétrole (en équivalent primaire).
14% par an, après tout, cela pourrait ne faire peur à personne, surtout que nous y sommes assurément depuis le démarrage de l’éolien.
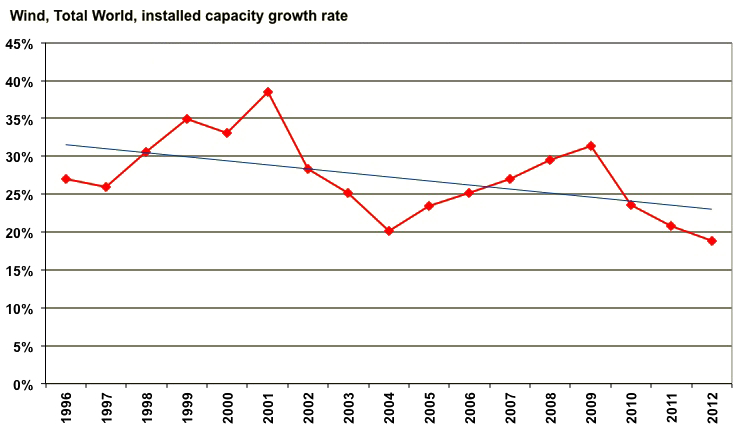
Taux de croissance de la capacité installée en éolien de 1996 à 2012.
Données BP Statistical Review 2013
Mais, à nouveau, faisons un peu d’histoire : pendant combien de temps les énergies fossiles, dont il faut rappeler qu’elles ont remplacé les énergies renouvelables préexistantes (et il doit y avoir une raison !), ont-elles eu un taux de croissance supérieur à 14% ? Réponse : pas si longtemps que cela…
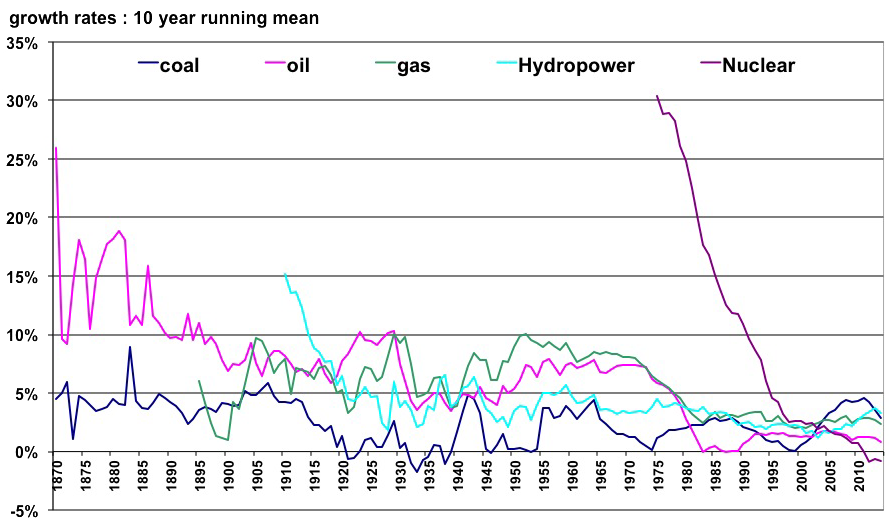
Taux de croissance annuel moyen des différents types d’énergie depuis 1860, en moyenne glissante sur 10 ans.
Exemple : la valeur pour 1960 représente le taux de croissance annuel moyen pour la période 1950-1960. La valeur pour 1940 représente les taux de croissance annuel moyen pour la période 1930-1940, etc.
A l’exception du pétrole à ses tous débuts (il représentait alors quelques % de l’approvisionnement mondial) aucune source majeure n’a connu de croissance annuelle moyenne supérieure à 10% pendant 50 ans. Dès qu’une énergie devient « mature », son taux de croissance annuel moyen tombe sous 5%, et il faut rappeler que ces % de croissance ont eu lieu dans un monde à la productivité structurellement croissante parce qu’il y avait de plus en plus d’énergie à la disposition de chacun.
Du coup, cela devient une hypothèse audacieuse que de penser que des énergies inconfortables d’emploi (comme le vent, peu concentré, intermittent et fatal) vont pouvoir croître plus vite, en tendance longue, que des énergies « faciles » (comme les combustibles fossiles, très peu chers à l’extraction, et capable de donner de grandes quantités de puissance à la demande), au surplus dans un monde où la productivité du travail « physique » devrait décroître… précisément parce que les énergies concentrées sont moins disponibles (or c’est cette productivité qui compte pour construire des centrales ou des raffineries, ou… des éoliennes).
Source : Schilling et. al et BP Statistical Review pour les données primaires, taux de croissance calculés par votre serviteur.
Dit autrement, le pronostic le plus probable est que l’éolien, dès qu’il va « sortir de l’épaisseur du trait », va ralentir fortement son taux de croissance (il y a d’excellentes raisons physiques à cela). Et le même raisonnement peut s’appliquer au photovoltaïque, qui représente aujourd’hui un dixième de l’éolien, ou… 0,07% de l’approvisionnement énergétique mondial !
Cette baisse du taux de croissance en valeur absolue ne signifie bien sûr pas que la part va baisser : si l’éolien reste à son niveau actuel mais que les combustibles fossiles voient leur contribution divisée par 4, la part de l’éolien augmentera mécaniquement. Mais en pareil cas on vérifiera aisément que l’hypothèse de départ d’une croissance économique de 2% par an n’est pas tenue !
- Vient ensuite le nucléaire : une multiplication par 7 de la production revient à disposer, d’ici 40 ans, d’un parc de 3.000 réacteurs de 1000 MW en service. C’est l’équivalent du nombre actuel de centrales à charbon, ou encore un peu plus de 10.000 milliards de dollars 2010 d’investissements. Sachant que le PIB mondial tourne actuellement autour de 60.000 milliards par an, ce n’est pas complètement ridicule en termes purement économiques, et par ailleurs pas complètement incompatible avec les ressources connues en matériaux fissiles ou fertiles, mais suppose de déployer très rapidement de la surgénération. Et si nous voulons « décarboniser » complètement l’économie avec essentiellement du nucléaire parce que les petits calculs ci-dessus montrent que ça ne passera pas facilement du côté des renouvelables à ces échelles de temps, c’est du double au quadruple qu’il faut avoir.
Peut-on être à la fois sérieux sur le climat et sur le PIB ?
Bien entendu, une autre alternative est de considérer d’entrée de jeu la décroissance de la consommation matérielle par individu comme normale (ce qui inclut aussi les services qui nécessitent des minerais ou de l’énergie). Cela revient à accepter la mise au régime comme une évolution souhaitable de nos sociétés. Nous n’en voulons pas, bien sûr, comme déjà Tocqueville l’avait indiqué. Mais même si nous le refusons, pouvons nous l’éviter ?
Il se trouve que la division par trois des émissions de CO2 (terme de gauche de notre équation de Kaya) est inéluctable « un jour« . En effet, lorsque nous avons des stocks de ressources donnés une fois pour toutes (le stock de combustibles fossiles et le stock de forêts sont dans ce cas), les mathématiques imposent que la consommation annuelle issue de ces stocks partira de zéro (ça c’est facile à vérifier !), passera par un maximum puis tendra à nouveau vers zéro avec le temps. Et, à l’évidence, les émissions de CO2 provenant de l’utilisation des combustibles fossiles suivront le même chemin.
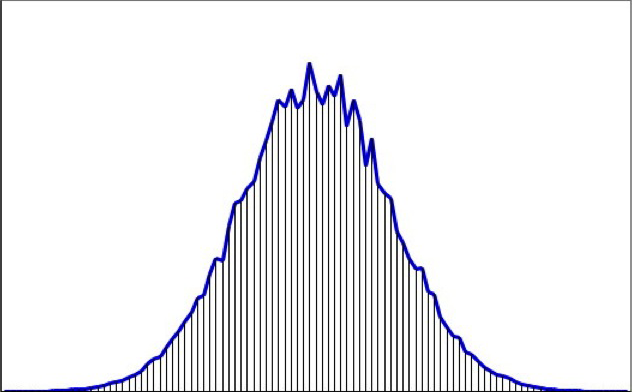
Aspect général de l’extraction d’une ressource dont le stock de départ est donné une fois pour toute.
La surface hachurée sous la courbe représente le cumul de l’extraction, et sa valeur du début à la fin est au plus égale au stock extractible de départ (qui, pour le pétrole, s’appelle une réserve ultime).
Les émissions humaines de CO2 auront donc aussi cet aspect. La seule question concernant le maximum est de savoir quand au plus tard il surviendra, à quel niveau, et quel type de processus nous fera passer ce maximum (notre volonté, ou l’effondrement de la société industrielle… tout est possible !). Mais il arrivera, c’est certain !
Or dire que les émissions de CO2 « tendront un jour vers zéro avec le temps » implique que, « un jour », les émissions mondiales de CO2 seront pour toujours inférieures au tiers de la valeur actuelle. La seule question est de savoir quand et dans quel contexte cela arrivera, mais cela arrivera de manière absolument certaine.
Dans ce genre de contexte, qui au surplus a toutes les chances d’être récessif, il n’est pas sûr que les ingénieurs parviennent à aller assez vite sur la « technique » (car le terme TEP/PIB désigne de manière synthétique tout ce que les ingénieurs savent faire pour proposer des voitures, des cafetières, et des maisons plus économes) et sur « l’énergie sans carbone » (car le terme CO2/TEP désigne de manière synthétique tout ce que les ingénieurs savent faire pour augmenter la part des renouvelables et du nucléaire dans l’offre énergétique) pour permettre une division par 9 à temps du « contenu en CO2 de l’économie ». Cette division par 9 est pourtant indispensable pour avoir à la fois la croissance économique ET la baisse des émissions de CO2 (qui finira par gagner).
L’égalité devant rester vraie, cela signifie alors que la division par 3 de l’ensemble des termes de droite « un jour » a toutes les chances (si l’on peut dire) de provenir d’une baisse des termes POP et/ou PIB/POP, et cela sera d’autant plus vrai que nous aurons tardé à prendre le taureau par les cornes pour « décarboner l’économie ».
Ironie de cette affaire, les élus qui aujourd’hui préconisent de s’occuper d’abord de la sortie du nucléaire pour rendre le monde plus stable sont au contraire en train de faire exactement ce qu’il faut pour accélérer la survenue de troubles économiques massifs qui rendront le monde bien plus dangereux, puisqu’ils contribuent à ce que la baisse des émissions de CO2 se reporte plus violemment sur le PIB par personne et la population. Ce n’est pas le moindre des paradoxes, j’imagine, pour le militant écologiste sincèrement convaincu que le nucléaire est la pire des calamités que de lui dire que de se débarrasser des centrales nucléaires civiles augmente les risques de guerre et de famines !
Pour en revenir à la règle de trois, cette dernière est aussi impitoyable avec les économistes classiques : avec ce fichu PIB, la décroissance sera très difficile à éviter, non point parce qu’elle serait désirable, mais parce que, hélas pour nous, le monde est fini. De ce fait, il serait sage d’arrêter de se focaliser sur cet agrégat macroéconomique auquel nous avons fait dire des tas de choses qu’il ne dit pas. Conserver comme étalon un indicateur qui va très vraisemblablement se mettre à aller – pour des raisons mathématiques – de plus en plus souvent dans le sens inverse de celui souhaité n’est pas compatible avec la gestion positive des sociétés humaines. Il vaudrait mieux passer à autre chose !